Термином комплексного числа (далее в тексте - КЧ) пользуются для обозначения выражений виды: ċ=а+jb, в которых индекс "ċ" используется для обозначения КЧ, а "а" и "b" отображают действительную и мнимую части. Значение "j" обозначает мнимую единицу и равно √(-1).
В английском языке словом Real принято характеризовать действительность, а термином Imaginary - мнимые свойства. От этих слов были созданы обозначения Re и Im, которые используются для выражения величин "а" и "b" следующим способом:
а=Re(с), b=Im(с).
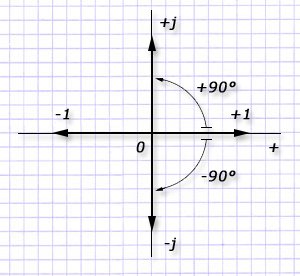
Для геометрического отображения КЧ в векторной форме применяется комплексная плоскость. У нее горизонтальная ось помечается знаком +1, а вертикальная – символом +j. Термин действительной (реже вещественной) части используется для наименования горизонтальной оси, а для вертикальной - мнимой.
Обе составляющие (действительная и мнимая) КЧ являются прямоугольными проекциями вектора на соответствующие оси.

В представленном графике значение с=|ċ| именуется модулем КЧ и равно длине вектора. Другим параметром, определяющим положение радиус-вектора, является его угол поворота α от оси +1 до текущего положения ċ, считающийся аргументом. α=arqċ.
Катеты треугольника представляются через соотношения:
a=cosα, b=csinα.
Используя тригонометрическую форму для выражения КЧ можно представить его видом:
ċ=с(cosα+jsinα).
Используя формулу Эйлера ejα= cosα+jbsinα, можно получить значение модуля в показательной форме ċ=сejα.
В полярной форме выражение имеет вид:
ċ=с∠α.
Положение единичного вектора можно изобразить на комплексной плоскости:
Мнимая единица имеет свойства:
j=ej90°, j2=-1=ej180°, j3=jj2=-j=ej270°=e-j90°, j4=j2j2=1=ej0=ej2Π, 1/J=1j/Jj=J/-1=-j.
К КЧ применимо понятие сопряжения. Им называют те числа, которые равны по величине модулей и аргументов, но имеют разные знаки у аргументов.
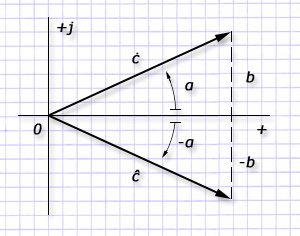
ċ=a+jb=cejα, ĉ=a-jb=cejα.
Из графика видно, что изображенные векторами КЧ симметричны по отношению к горизонтальной оси.
КЧ и математические действия. Для их сложения или вычитания делается запись в алгебраическом выражении:
ċ=ċ1+ċ2=(a1+jb1)+(a2+jb2)=(a1+a2)+j(b1+b2)=a+jb.
В этом соотношении отдельно суммируются мнимые и вещественные составляющие: а=а1+а2, b=b1+b2.
Данные алгебраические сложения чисел выражают выполнение сложения соответствующих им векторов.
Выполняя сложение сопряженных чисел можно заметить, что их сумма выражается удвоенным значением вещественной составляющей:
ċ+ĉ=(а+jb)+(а-jb)=2а.
Выражения КЧ в показательной форме удобны для выполнения умножения или деления. При этом у них модули перемножают или делят, значения аргументов складывают либо вычитают.
ċ=ċ1ċ2=c1ejα1c2ejα2=c1c2ej(α1+α2)=cejα; ċ=ċ1/ċ2=c1ejα1/c2ejα2=c1ej(α1-α2)/c2=cejα.
В выражении с=с1/с2, α= α1-α2.
Нетрудно заметить, что при действии умножения длина вектора увеличивается в величину с2, а аргумент - на значение а2. При представлении КЧ векторами соблюдается закономерность: для умножения вектора на КЧ вида aеjα достаточно растянуть вектор в а раз и довернуть на угол α.

Для вычисления произведения сопряженных чисел достаточно взять квадрат их модуля:
ċĉ=(а+jb)(а-jb)=а2+b2, или ċĉ=сejαсe-jα=с2.
Для перемножения и деления КЧ при определенных условиях удобно пользоваться их алгебраическим выражением. В таком виде действия проводятся по законам умножения многочленов и учете значения j2=-1.
ċ=ċ1ċ2=(a1+jb1)(a2+jb2)=(a1a2-b1b2)+j(b1a2+a1b2).
Для деления чисел достаточно избавиться от значения j в выражении знаменателя методом перемножения знаменателя и числителя на одно и то же выражение сопряженного знаменателя:
ċ=ċ1/ċ2=((a1+jb1)/(a2+jb2))((a2-jb2)/(a2-jb2))=((a1a2+b1b2)+(b1a2-a1b2))/(a22+b22)=a+jb; a=(a1a2+b1b2)/(a22+b22); b=(b1a2-a1b2)/(a22+b22).
Графики построенных векторных диаграмм могут иметь изображение:
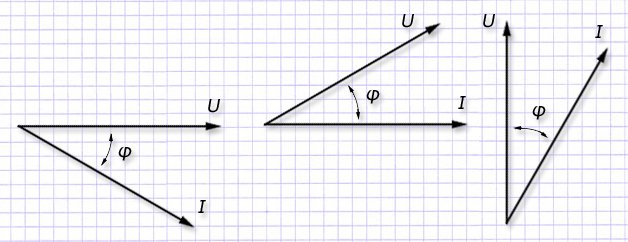
Для выражения значения тока с синусоидальной формой пользуются соотношением i=Imsin(ωt+ψ), которым изображают на комплексной плоскости вектор с длиной Im и углом наклона ψ к горизонту. Его выражение Im=Imejψ считают комплексной амплитудой для тока. представляют графиком:

Чтобы получить действующую величину для тока требуется комплексную амплитуду разделить на √2.
İ=İm/√2=ejψIm/√2 =Iejψ.
В электротехнике заглавные буквы с расположенными над ними точками (E, U, I) используются для обозначения КЧ, выражающих синусоидальные зависимости от времени ЭДС, напряжения и тока.
Обозначение комплексной проводимости и сопротивления делается прописными буквами Y и Z, для показа их модулей используется строчное написание у и z. Обозначение комплексной мощности выполняется символом S со значком тильда "҇" над ним.