Термином действующего значения для тока пользуются с целью выполнения измерений. Гармоники переменных величин не похожи одна на другую, отличаются многими параметрами.
Если учитывать только амплитуды, то сравнивать можно исключительно одинаковые по частоте и форме синусоиды. В практической деятельности это не приемлемо потому, что токи с равными амплитудами у синусоид, отличающихся по частоте и форме, совершают разное действие.
Для анализа переменных токов принято использовать создаваемую ими работу. Такой метод позволяет анализировать даже воздействия постоянного и переменного токов, которые на определенном участке цепи выделяют теплоту.
По ее величине и оценивают силу тока. К примеру, если переменный ток нагревает электрическую цепь так же, как и постоянный аналог в 1 ампер, то считают, что сила переменного тока – 1A. Такое соотношение именуют действующим значением.
Оценивают действующие значения переменных токов по численным величинам постоянных токов, которые в течение продолжительности одного периода времени создают равное выделение тепловой энергии в таком же точно сопротивлении. Замер величины переменного тока по данной методике предполагает:
1. Вычисление значения теплоты, выделяемой в сопротивлении (R) в течение периода времени T в случае протекания по нему переменного тока (i) по соотношению:
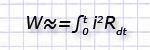
2. Выяснение величины постоянного тока (I), могущей за такое же время T нагреть сопротивление R таким же объемом теплоты по соотношению: W=I2RТ.
3. Сопоставления теплоты:
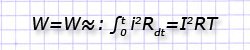
И получения:
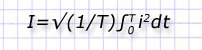
Полученное соотношение оценивает действующую величину для переменного тока. Для примера на вход электрической цепи подадим напряжение импульсного характера с треугольной формой.
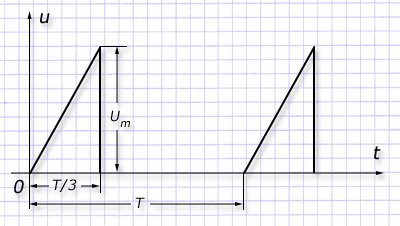
Определить значение действующей величины напряжения в данном случае можно выражениями:
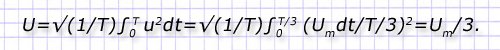
В другом примере используем схему однофазного выпрямителя, убирающего одну полуволну синусоиды:
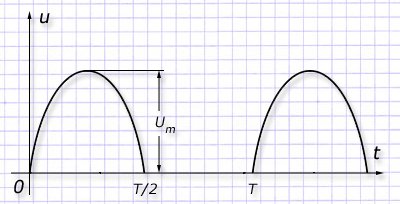
Требуется найти действующее значение для такого напряжения при известной величине амплитуды в 311 вольт. Решение будет следующим:
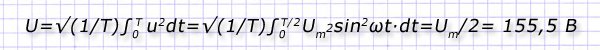
В третьем случае рассмотрим расчет обыкновенного синусоидального тока, характеризуемого выражением: i=Imsin(ωt). Решение для него очевидно:
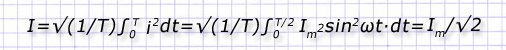
По результатам приведенных примеров демонстрируется зависимость величины переменного тока от формы гармоники.