Определения самоиндукции и индуктивности, синусоидальный ток в индуктивностях

Когда по обмотке катушки проходит электрический ток i, то им формируется в каждом витке магнитное поле, называемое потоком самоиндукции. Для его обозначения принят символ Ф_L. Поток индуцирует на выводах обмотки ЭДС, называемую электродвижущей силой самоиндукции, которая обозначается е_L.

Ее величина вычисляется по формуле е_L=-dΨ/dt.

Значение потокосцепления Ψ при возникновении самоиндукции определяется величиной проходящего сквозь витки обмотки тока по выражению: Ψ=Li.

Индуктивность L характеризует пропорциональность между проходящим через обмотку катушки током и потокосцеплением. Она зависима от:

   - применяемой формы катушки;
   - габаритов конструкции;
   - значения магнитной проницаемости у сердечника.

Для определения индуктивности принята единица генри: Гн. 1 Гн соответствует индуктивности электрической цепи, в которой возбуждается ЭДС в 1 вольт за время 1 секунды при отклонении скорости тока на 1 ампер.

Обычно, индуктивность постоянна и характеризует способности катушки. С учетом индуктивности формула для ЭДС получает вид:

   е_L=-Ldi/dt.

Для обозначения в электросхемах индуктивности принято понятное изображение.

Индексом U_L принято обозначать разность потенциалов на клеммах обмотки, которая появляется под действием ЭДС самоиндукции, то есть напряжение, созданное в обмотке переменным результирующим магнитным полем всех витков.

При обозначении на схемах принято показывать направления тока i, напряжения U_L и ЭДС e_L в одну сторону. На самом деле направления ЭДС и напряжения противоположны.

   U_L=-е_L=Ldi/dt.

Отрицательный знак напряжения по отношению к ЭДС объясняет правило Ленца, разъясняющее, что направление электродвижущей силы самоиндукции препятствует причинам, обусловливающим ее возникновение.

Причиной возникновения ЭДС является изменение протекающего синусоидального тока по обмотке. Возрастающая часть гармоники по направлению совпадает с увеличением синусоиды ЭДС, а уменьшающаяся - с понижением.

ЭДС самоиндукции препятствует изменениям тока, создает сопротивление на его пути, которое называют индуктивным, обозначают X_L.

   X_L=ω∙L=2Πf∙L.

Значение индуктивного сопротивления зависит от скорости изменения переменного тока и индуктивности. У постоянных цепей магнитные поля постоянны, не меняются, ЭДС самоиндукции отсутствует.

Мгновенное значение величины напряжения можно выразить формулой через значение тока, протекающего сквозь индуктивность.

   u_L=L∙I_m∙ωcos(ωt+Ψ)=U_Lm∙sin(ωt+Ψ+90°).

От мгновенных величин можно перейти на амплитудные:

   U_Lm=I_m∙ωL=I_m∙X_L.

Для выражения действующих значений производим деление амплитуд на _√2.

   U_L=I∙ωL=I∙X_L, где I=UL/X_L=U/ωL=В_L∙U.

   В_L=1/X_L=1/ωL. Величине В_L присвоено название индуктивной проводимости.

Записанные в символической форме уравнения соответствующих формул имеют следующий вид:

   Ù_Lm=U_Lme^j(Ψ+90°)=U_Lme^jΨe^j90°=I_mx_Le^jΨj.

Поскольку I_me^jΨ=İ_m, то Ù_Lm=İ_mjx_L=İ_mjωL.

Получаем İ_m=Ù_Lm/jx_L=Ù_Lm(-jB_L).

Выражения действующих значений: Ù_L=İjx, İ=Ù_L/jx_L.

Связи между напряжением и токами в индуктивностях описаны законом Ома, выражаются комплексными числами или вещественными значениями.

Для индуктивностей характерен сдвиг начальной фазы гармоники напряжения вперед по ходу вращения на четверть периода от направления тока. Это положение формулируют отставанием тока от напряжения на угол в 90°.

Аналогичное действие с векторами получается при их умножении на значение "j". Векторные величины токов и напряжений можно представить на диаграмме.

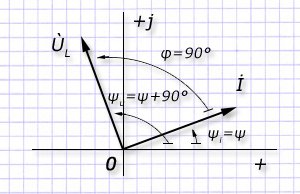
Из выражения U_L понятно, что оно в индуктивности получается при умножении значения Ix_L на величину j, которая вращает вперед вектор напряжения относительно направления тока.

Рассмотрим на частном примере способ построения векторных диаграмм и определение мгновенных значений токов в индуктивности по мгновенным выражениям напряжения.

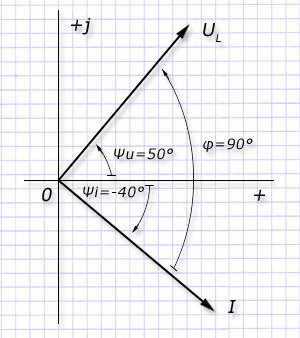
Допустим, u_L=220 sin(ωt+50°)В. Величина индуктивности составляет 12,739 мГн.

Для частоты промышленной электросети в 50 герц выражение угловой скорости ω=314 с-1. Х_L=ωL=314∙0,001274=40 Ом.

Амплитудное значение получим выражением I_m=220/40=5,5 А.

Значение начальной фазы тока в индуктивности отстает от напряжения по выражению:

   ψ_i=ψ_u–90°=50–90=–40°.

Получаем выражение мгновенного значения: i=5,5 sin(ωt–40°). Его диаграмма будет иметь вид: