Рассмотрим пару катушек имеющих кольцевую намотку проводниками.
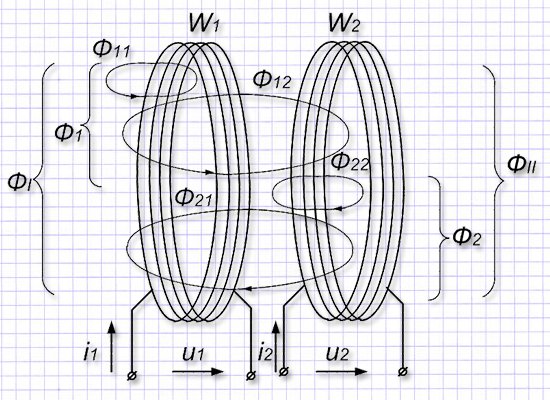
Активные сопротивления каждой обмотки очень близки к нулевым значениям, ими пренебрегаем, а количество витков обозначим W1 и W2. Расстояние между обмотками взято таким образом, что магнитные поля у них пересекаются. Это наглядно демонстрирует рисунок, где отражено движение токов i1 и i2 с их магнитными полями.
Каждая кольцевая линия Ф на рисунке имеет двойное цифровое обозначение, символизирующее отдельный магнитный поток. У него 1-ая цифра индекса указывает катушку-генератор потока, а следующая уточняет, на какие обмотки он еще действует.
Первая катушка генерирует потоки:
- Ф11 – собственный, не влияющий на соседний; - Ф12 – дополнительный, охватывающий рядом расположенную катушку W2.
Вместе они образуют поток самоиндукции Ф1, который дополняется еще одной величиной: потоком взаимной индукции, идущим от соседней обмотки у второй катушки.
Сложив эти три составляющие (Ф11, Ф12, Ф21), получаем суммарное значение Фӏ, включающее все действующие в катушке виды потоков от самоиндукции и взаимоиндукции.
По другому их можно выразить соотношением: ФI=Ф1±Ф21. При этом следует обратить внимание на знак перед Ф21, который зависит от его направленности по отношению к магнитным полям первой обмотки. Если она противоположна для Ф1, то выражение меняется на ФI=Ф1–Ф21. Именно такая ситуация изображена в нашем случае.
Поскольку данная форма катушки предполагает всего лишь один магнитный поток, воздействующий на нее, то найти ее полное потокосцепление не составит труда:
Ψ1=W1·Ф1=W1·Ф1±W1·Ф21=Ψ1±Ψ21,
где Ψ1=W1·Ф1 и Ψ2=W1·Ф21 – потокосцепления само- и взаимной индукции соответственно.
Оба они пропорциональны току, вырабатывающему их: Ψ1=L1·i1 и Ψ21=Мi2. Подставляя данные значения в вышеприведенную формулу, получим ΨI=L1·i1±М·i2.
Изменение потока неизменно провоцирует появление у нее ЭДС электромагнитной индукции, которая обеспечивает выработку напряжения на местах зажимов:
u1=dΨ1/dt=L1·di1/dt±M·di2/dt.
Запись в символической форме выражения будет выглядеть следующим образом:
Ù1=İ1·j·ψ·L1±İ2·j·ψ·M=Ù1L+Ù1M.
Все сказанное одинаково справедливо для обеих катушек, поэтому их уравнения аналогичны.
Здесь, значение Ù1L – не что иное, как напряжение самоиндукции. Оно создано катушкой самостоятельно.
Напряжение Ù1M – добавочное, выработанное на ее зажимах от изменения поля соседней обмотки (взаимной индукции).
Так же, как и ранее, при согласном подключении обмоток знаки совпадают, а при встречном – противоположны.
Для определения взаимной индукции разработан такой термин, как "одноименные зажимы". Он помогает рассчитать движение потоков катушек, узнать характер их включения, достоверно изображать на схемах и одинаково обозначать в реальной конструкции.
На обмотках катушек зажимы называют одноименными, если существуют токи одного направления в них, наводящие в витках каждой из отдельно взятых обмоток магнитные потоки, которые складываются (как от само-, так и взаимной индукции.
То есть катушкам, на которых заранее достоверно известны окончания и начала витков при выполнении условия одинаковой направленности токов с образованием магнитных потоков в одну сторону, свойственно согласное подключение обмоток.
Выполнение тех же условий, но движение магнитных потоков в разные стороны, свидетельствует о встречном включении.
Если известно о существовании магнитной связи между двумя обмотками, то ее изображают на схеме простой полукруглой двусторонней стрелкой, обозначенной i1.