Представим себе участок электрической схемы, на который приложено напряжение u, создающее электрический ток в цепи i. За отрезок времени dt током i будет перемещен заряд электричества dq=i∙dt, который создаст мощность величиной р=dwdt=u∙i.
Ее называют мгновенной мощностью, используют для выяснения направлений и скоростей движения энергии на определенных участках электрических цепей.
Энергия может поступать внутрь электросхемы или уходить из нее. Для определения ее направления принято процесс накопления обозначать положительным знаком, а расходования – отрицательным.
При положительной мгновенной мощности ток и напряжение обладают одинаковыми знаками, а разное их направление создает отрицательную производную, характерную для случая разряда емкости, когда энергия накопленного конденсатора возвращается назад к источнику.
Следует учитывать, что энергия может не поступать на источник, а расходоваться на преобразования в механическую работу или тепловыделения. Ее количество определяет закон Джоуля-Ленца, который можно выразить за время одного периода колебания синусоидального тока выражением (а):
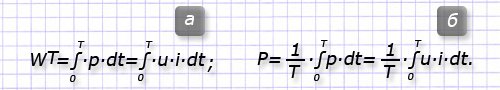
Если ее выразить за время Т (разделить на Т), то получим среднюю величину мгновенной мощности в течение периода, которую называют активной мощностью (б):
Физическое определение этой величины состоит в выражении энергии, выделяющейся в виде механической или тепловой работы за определенную единицу времени. Выразим гармоники тока и напряжения через синусоидальные функции:
c i=Im∙sinωt, u=Umsin(ωt+φ).
Подставим их в выражение активной мощности, после преобразования получим уравнение Р=U∙I∙cosφ.
Воспользуемся соотношениями сторон для треугольников токов, напряжений, проводимостей и сопротивлений для выражения через электрические характеристики значения активной мощности, которая будет представлена видом:
c P=I2zcosφ=I2R=U2ycosφ=U2G=UaI=UIa.
Теперь можно рассмотреть электрические процессы, происходящие в отдельных элементах цепи.
У активного сопротивления вектора напряжения и тока имеют одинаковую фазу, когда угол φ=0. Для любого временного момента они имеют одинаковое направление, что свидетельствует о чисто положительном значении мгновенной мощности.
Это означает следующее: у активного сопротивления поступающая электроэнергия преобразуется в тепло либо механическую работу. Активная мощность выражается соотношением:
P=I=I2R=U2G.
Для реактивных нагрузок создается другая ситуация, когда угол сдвига фаз между векторами достигает 90°. У индуктивностей при отставании тока он имеет положительное значение, а у емкостей - отрицательное.
Подставим значение φ=±90° для входного напряжения в схему, получим значение u=Um∙sin(ωt±90°)=±Um∙cos(ωt).
Это выражение характеризует изменение мгновенной мощности во времени по синусоидальному закону, но с увеличенной, двойной частотой колебаний сети - р=±U∙I∙sin2ωt. То есть, дважды за половину периода она меняет свой знак.
Если подставить это значение в выражение активной мощности, то получится результат Р=0, что означает отсутствие необратимых преобразований электроэнергии в механическую и тепловую у реактивных элементов.
У индуктивных нагрузок во время 1-й четверти периода колебания, когда ток Im возрастает, наблюдается накопление магнитного поля у индуктивности. Энергия Wм=LI2m/2.
За время прохождения следующей четверти идет уменьшение тока до нулевого значения, а энергия от магнитного поля направляется назад к источнику внешней цепи.
Такие же процессы наблюдаются у емкости. При возрастании напряжения на обкладках конденсатора в течение 1-го периода происходит заряд емкости и накопление энергии электрического поля Wз=С∙U2m/2, а в последующей четверти периода осуществляется разряд у конденсатора, когда накопленная им энергия возвращается назад в схему.
При этом, идет взаимообмен энергиями между магнитным полем электрической цепи с полем конденсатора. Поэтому ее называют энергией обмена.
Значения энергий магнитных Wм и электрических WЭ полей выражают следующие соотношения:
WM=LI2/2=(L(I√2)2/2)∙ω/ω=I2ωL(1/ω)=I2xL(1/ω)=QL∙(1/ω); WЭ=CU2m/2=(C(U√2)2/2)∙ω/ω=U2ωC∙1/ω=I2∙1/ω∙(1/ωC)=I2xC∙(1/ωC)=QC∙(1/ωC).
У приведенных выражений значения QL=I2∙XL и QC=I2∙XC имеют размерность мощности. Их называют реактивными мощностями индуктивности и емкости соответственно.
Следует понимать, что они не совершают работу, а просто представляют собой величины, пропорциональные энергиям соответствующих магнитных и электрических полей QL=ω∙WM, QC=ω∙WЭ.
Электросхемы, содержащие в своем составе емкости и индуктивности, претерпевают колебания электроэнергии от реактивных нагрузок.
Причем, если электрическое поле конденсаторов набирает энергию в какой-то момент времени, то магнитное поле катушек индуктивности в эти мгновения ее отдает. В последующую четверть периода процесс изменяется на противоположный.
Это означает, что энергии магнитного и электрического полей обладают противоположными знаками: положительному направлению энергии индуктивности соответствует отрицательное направление магнитной, и наоборот.
Выражение суммарной энергии для электрического и магнитного полей за время четверти периода можно выразить соотношением:
WЭМ=WM-WЭ=LI2m/2-CU2m/2=(1/ω)(Q-QC)=Q∙1/ω.
В полученном соотношении значение Q выражает реактивную мощность цепи, которая пропорционально зависима от энергии электрических и магнитных полей. Q можно определить с помощью выражений ее реактивных сопротивлений.
Q=QL-QC=I2∙(хL-хC)=I2∙х.
Для случая резонанса сопротивления ХL=ХC, наблюдается равенство реактивных мощностей QL и QC и энергий WM и WЭ, которые заключены в электрических и магнитных полях. Поэтому, между емкостями и индуктивностями при резонансе обмен энергиями происходит без участия внешних источников.
Вычислить реактивную мощность можно по формуле:
Q=I2∙х=I2∙z∙sinφ=U∙I∙sinφ=U2∙y∙sinφ=U2∙В=Uр∙I=U∙Iр.
В расчетах электрических схем при анализе происходящих процессов используют треугольник мощностей.
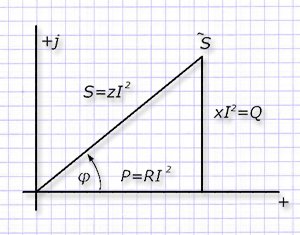
Его получают умножением каждой стороны у треугольника сопротивлений на значение квадрата тока. У него наблюдается такое же соотношение сторон:
cosψ=P/S; sinψ=Q/S; tgψ=Q/P.
Индексом S обозначают полную мощность, которая представляет собой гипотенузу. Ее выражают соотношением:
S=√(P2+Q2)=I2z=U2y=UI.
Величина полной мощности определяет ту часть электрической энергии, которую вырабатывает внешний генератор и отдает в электрическую схему. Она влияет на габариты и материалы электрических приборов и машин.
Состояние изоляции, толщину изолирующего слоя и расстояния между токоведущих частей определяет величина напряжения. А сила тока влияет на выбор материала токопроводов, их поперечное сечение, возможности отвода тепла для охлаждения электрических приборов.
Из графика хорошо видно: величина полной мощности достигает максимального значения при угле φ, косинус которого равен 1, что характерно для выражения активной.
Для обозначения мощностей в разных нагрузках используются одни размерности, но с разными названиями. Активную измеряют ваттами (Вт), реактивную - вольт-амперами реактивными (вар), полную - вольт-амперами (ВА).
С целью определения комплексной мощности требуется умножить комплекс напряжения на сопряженный комплекс соответствующего тока:
Ũ=Ùİ.