Резонансные явления в электрических цепях

При протекании электроэнергии по элементам электрической схемы возможно возникновение различных режимов; совпадение по фазе вектора токов и напряжений в цепях с емкостью и индуктивностью называют явлением электрического резонанса.

При нем исчезает реактивный характер нагрузки и выполняются все соотношения для активного сопротивления, когда Х=I_m∙Z, В= I_m∙Y, R=Z, φ=0.

В электротехнике при последовательном соединении элементов индуктивной и емкостной нагрузки возможен резонанс напряжений. Рассмотрим его проявление для простейшей цепи с последовательно образованным контуром, когда резонанс проявится при случае Х=Х_L-Х_C=0. Выразим Х_L=Х_C, а после подстановки их выражений получим соотношение:

   φL=1/φC.

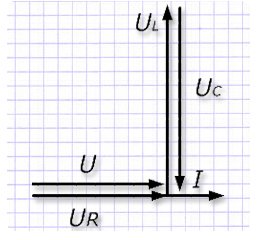У индуктивности и емкости для рассматриваемого случая вектора напряжений находятся в противоположных фазах, уравновешивают друг друга. При этом, все напряжение, которое приложено на электрическую схему, воздействует на активное сопротивление. Диаграмма векторов представлена следующим видом:

Диаграмма демонстрирует, что величины напряжений на реактивных нагрузках при резонансе могут весьма значительно превышать входное напряжение схемы. Для оценки этого параметра введено термин добротности контура Q.

   Q=U_L/U=U_C/U=x_Lрез/R=x_Cрез/R.

Она зависит от частоты, величины емкости или индуктивности. Изменяя любой из перечисленных параметров можно регулировать величину добротности. В радиотехнике она нашла широкое применение, где ее величина доводится до больших значений в несколько сотен единиц во время резонанса напряжений.

При этом возникают изменения реактивного и полного сопротивлений в схеме, следствием чего проявляются изменения токов, напряжений, углов сдвига фаз на различных приемниках электроэнергии.

Зависимость параметров электрической схемы при изменении значений емкости С_O для создания резонанса демонстрирует график:

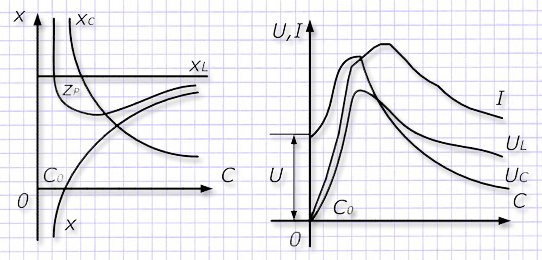
Величину С_O выражает соотношение: С_O=1/(ω2L).

Вполне допустимо рассмотреть случай параллельного соединения нагрузок R, L и C. Для него будет справедлива векторная диаграмма вида:

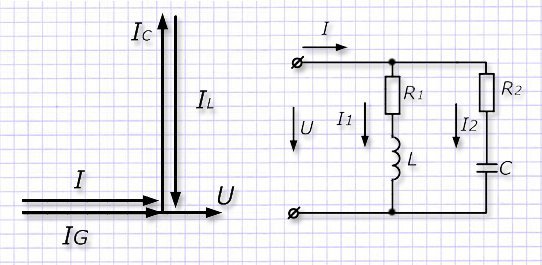
На практике приходится иметь дело с более сложными соединениями элементов. Для примера можно взять разветвленную схему с 2-мя параллельными ветвями, включающими как активные, так и реактивные нагрузки.

У данной цепи резонанс наступает при равенстве нулю составляющей ее реактивной проводимости, когда I_m∙Y=0. То есть, при рассматриваемом случае мнимая часть у комплексного выражения Y приравнена к нулю.

Найдем значение комплексной проводимости для схемы, которая выразится суммой всех проводимостей в ветвях.

   Y=Y1+Y2=1/Z1+1/Z2=1/(R1+jx1)+1/(R2-jx2)=(R1-jx1)/(R²1+x²1)+(R2+jx2)/(R²2+x²2)=
   R1/(R²1+x²1)+R2/(R²2+x²2)-j(x1/(R²1+x²1)-x2/(R²2+x²2)).

Выражение, выделенное круглыми скобками, приравниваем к нулю и получаем соотношение:

   x1/(R²1+x²1)=x2/(R²2+x²2).

Данное соотношение может быть представлено развернутым видом:

   φL/(R²1+(φL)²)=(1/φC)/(R²2+(1/φC)²).

Мы получили выражение, не похожее на реактивные проводимости для 1-й и 2-й ветвей цепи с В1 и В2. Сделаем замену рассматриваемой нами схемы на эквивалентную. У нее значения параметров определены расчетом для условий резонанса, когда В=В1-В2=0:

Таким способом мы пришли к искомому выражению. Векторная диаграмма для полученной схемы разветвленной цепи может быть выражена так:

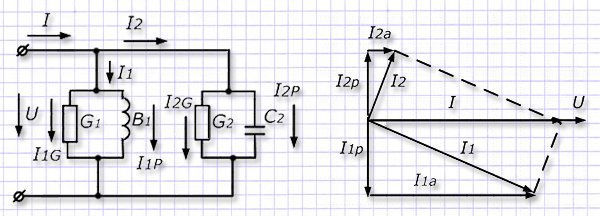
В разветвленных схемах возникает явление резонанса токов, когда реактивные части токов для противоположных ветвей направлены в противоположных направлениях и уравновешены между собой по величине. Общий ток в схеме формируется суммой составляющих активных токов в ветвях.