Для составления диаграммы выбираем комплексную плоскость и обозначаем прямоугольные декартовые координаты. Из их начала определяем положение произвольного вектора имеющего длину Im.
Его первоначальное положение на плоскости удобно определить углом ψ по отношению к направлению оси абсцисс.
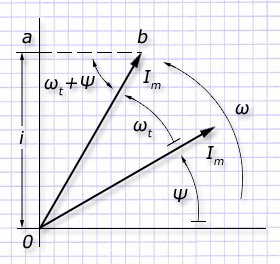
Придадим ему противоположное ходу часовой стрелки вращение с величиной угловой скорости ω. Через временной интервал t рассматриваемый вектор переместится к обозначенному положению угла ωt в точку “b”.
Спроектируем по простым законам математики его длину в данную точку “a” на ось ординат, обозначим проекцию индексом i. По тригонометрическим формулам прямоугольного треугольника с вершинами в точках “0”, “a”, “b” определим i=Imsin(ωt+ψ).
В данном соотношении получилось значение функции для выражения мгновенной величины тока, которая представляет проекцию на положительно направленную вертикальную ось системы координат для крутящегося вектора.
Подобно выполненные изображения векторных процессов называют векторными диаграммами, а длину представляемых величин принято представлять в разных системах измерений амплитудным либо действующим значением.
На практике удобно показывать положения векторов не на произвольных точках комплексной плоскости, а в самый начальный момент его движения при t=0, то есть при совершенно полных совпадениях углов их наклонов с начальными фазами.
По соотношениям вида:
- u=Umsin(ωt+Ψu); - i=Imsin(ωt+Ψi).
удобно выстраивать диаграммы токов и напряжений:
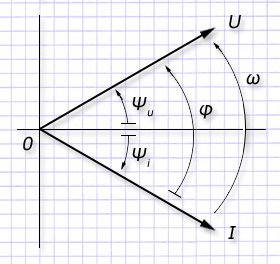
На полученных такими способами графиках длины векторов выражают действующие значения их величин, а углы их поворотов на комплексной плоскости - начальные фазы с разностью между ними, представленной углом сдвига рассматриваемых фаз φ=Ψu-Ψi.
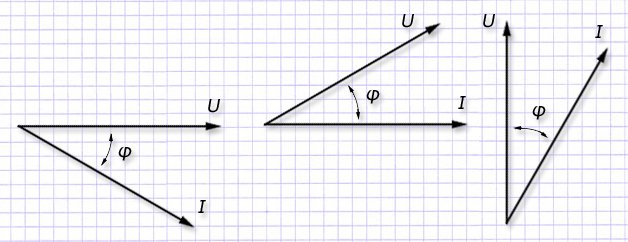
По действующим правилам построения диаграмм направление угла φ всегда выбирается от направления токов к направлению напряжений в сторону противоположного вращения часовой стрелки для обозначения положительного вращения.
Векторные диаграммы позволяют наглядно оценивать взаимное расположение синусоидальных величин переменного тока в системе координат.
При вращении диаграммы, представленной на схеме, в положительном направлении наблюдается отставание вектора тока от соответствующего ему напряжения на значение угла φ.
При практических расчетах для анализа рассматриваемых величин на диаграммах учитывают, что длины векторов, как и углы между ними, остаются неизменны для установившегося режима, причем начальные фазы обычно не показывают.
Применяемые упрощения позволяют нагляднее, доступнее представлять диаграммы, не изображать на плоскости их оси, размещать их в любой удобной форме для восприятия.