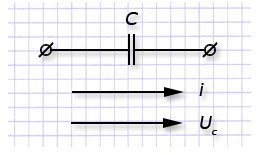
В электротехнике под термином "емкость" принято понимать конденсатор - конструкцию из двух проводников, разделенных между собой диэлектриком. Такие устройства способны при подключенной энергии накапливать заряды на проводниках, называемых обкладками конденсаторов.
Величина получаемого заряда q зависит от значения приложенного напряжения Uс и пропорциональна его величине: q=С∙Uс.
Коэффициент С, характеризующий пропорциональность между создаваемым зарядом и приложенным напряжением называют емкостью, измеряют в фарадах, обозначают символом Ф.
Размерность фарады определяется формулой:
кулон/вольт=ампер∙секунду/вольт=секунда/Ом=Ом-1∙с.
Величина емкости зависит от конструктивных особенностей конденсатора, его габаритов, толщины и диэлектрической проницаемости между пластинами диэлектрика.
Рассмотрим характеристики электрических синусоидальных процессов в конденсаторе. Пусть к его обкладкам приложено напряжение, представленное выражением: uс=Uс max∙sin(ωt+ψ).
В моменты его возрастания до максимальной величины от нулевого значения на обкладках конденсатора идет накопление заряда q, который при снижении напряжения до нуля стекает с пластин, что ведет к разряду конденсатора.
Получается, что при заряде и разряде конденсатора в подключенных к нему проводах движутся электрические заряды, или другими словами, протекает переменный электроток. При этом мы не рассматриваем процессы, возникающие между обкладками в конденсаторе.
Величина протекающего через конденсатор тока зависит от степени его заряда, проходящего в каждую единицу времени сквозь поперечное сечение провода:
i=dq/dt=С∙duс/dt.
Также, из формулы видно, что ток, проходящий через конденсатор зависит от емкости и быстроты изменения напряжения, подводимого к обкладкам, то есть от частоты сигнала. Характеристика конденсатора, выражающая зависимость между циклической частотой и емкостью принято называть емкостной проводимостью.
Для ее записи существует выражение Вс=ω∙С=2Π∙f∙С. Обратную проводимости величину называют емкостным сопротивлением:
хс=1/Вс=1/ωС=1/2ΠfС.
Проведем следующие математические операции:
i=С∙UСm∙ωcos(ωt+Ψ)=Im∙sin(ωt+Ψ+90°); Im=С∙UСm=Вс∙UСm.
И перейдем к выражению действующих значений:
I=С∙UС=Вс∙UС, значение UС=I∙1/ωС=I∙хС.
Мы получили выражения для законов Ома при протекании синусоидальных токов через конденсаторы. Представим их выражения в символической форме.
ÙC=UCm/√2=UC∙ejψ; Ì=Im/√2ej(φ+90°)=I∙ejf∙ej90°=ω∙C∙UС∙ejf∙j.
После выполнения преобразования получаем:
Ì=ÙCj∙1/ωС=ÙC∙j∙BC.
Откуда получим:
ÙC=i∙1/jωС=i(-j1/ωС)=i(-j∙xC).
По полученным выражениям построим в комплексной плоскости диаграмму векторных величин в емкости:
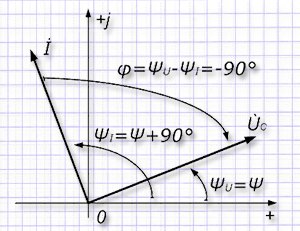
На ней каждый вектор имеет собственный угол наклона к направлению положительной вещественной оси. Это видно при умножении выражения Ixc на значение –j, когда получается вектор UС, повернутый к вектору тока на 90° по направлению движения часовой стрелки, то есть в отрицательную сторону.
На диаграммах направление угла φ всегда принимается от векторов тока в сторону векторов напряжения.
Далее, закрепим материал и рассмотрим практический пример. Допустим, на обкладки конденсатора подводится переменное напряжение, описываемое по закону: uC=150sin (1500t–45°).
Емкость конденсатора равна 100 мкФ. Требуется выразить мгновенное значение тока, пропускаемого через конденсатор и представить его значение при удвоении питающей частоты напряжения.
Вначале определимся со значением емкостного сопротивления.
хс=1/ωС=1/1500∙100∙10-6=6,667 Ом.
Далее, рассчитаем амплитуду тока:
Im=UCm/XC=150/6.667=7,49 A.
У нас в задании Ψu=-45°, а угол φ=-90°. Отсюда получим значение:
Ψi=Ψu-φ=-45°-(-90)=45°.
По результатам преобразований можем сделать запись:
i=7,49∙sin(1500t+45°).
При удвоении частоты значение емкостного сопротивления уменьшится вдвое:
хс=1/2ωС=3,333 Ом.
Это приведет к увеличению амплитуды тока: Im=UCm/XC=150/3,333=45,004 A.
Угол сдвига между фазами остался прежним. Мгновенное выражение для тока можно записать соотношением:
i=45,004∙sin(1500t+45°) А.