Под термином “фаза” в энергетике принято понимать отдельную часть электрической цепи многофазной системы или-же, момент времени в синусоидальном выражении векторов тока или напряжения.
Основная особенность многофазных (n) систем состоит в объединении отдельных схем с одинаковыми электрическими параметрами ЭДС, напряжения и тока, которые разнесены по времени на одинаковые интервалы периода ∆t=T/n выражаемые, также в угловых величинах фазы ∆ωt=360/n (в градусах) либо ∆ωt=2π/n (в радианах).
Трехфазные цепи. В энергетике применяются три объединенных электрических схемы (фазы), n=3. Соответственно все цепи разнесены на 120 угловых градусов. Для их обозначения в соответствии с ГОСТ-ом используются:
- заглавные латинские буквы А, В, С в качестве основного обозначения;- арабские цифры 1, 2, 3 для дополнительной маркировки;- заглавные латинские буквы R, S, T в международном формате.
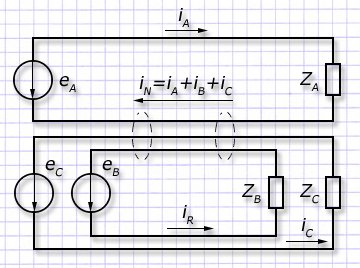
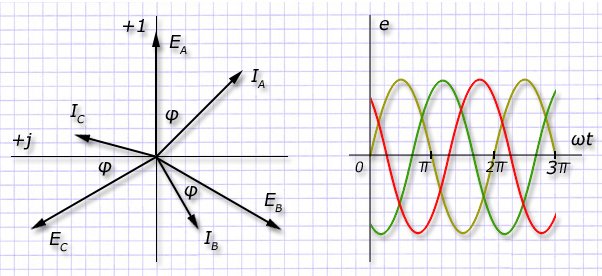
В процессе эксплуатации головная организация произвольно выбирает первую фазу “А”, а остальные нумерует в последовательности прохождения векторами напряжения (u) и тока (i) северного направления координат.
В трехфазной системе принято под прямой последовательностью понимать в нормальном режиме работы вращение векторов А>В>С>А против часовой стрелки. При этом, вектора в цепи В запаздывают от цепи А и обгоняют цепь С на 120°.
Противоположное вращение векторов по часовой стрелке считается обратной последовательностью.
Созданные в системе фазы могут объединяться в единую схему или работать изолированно, без взаимных связей. В не связанной системе величины мгновенных ЭДС в фазах разнесены по углу на 120° и чередуются по схеме А>В>С>А. Их значения описываются формулами:
eА=Еmsinωt, EА=Еej0°; eВ=Еmsin(ωt-120°), EВ=Еe-j120°; eС=Еmsin(ωt-240°)=Еmsin(ωt+120°), EС=Еej120°.
Диаграммы графиков функций и векторные выражения поясняются соответствующими рисунками.
В независимой симметричной 3-х фазной схеме всегда действует правило: любые переменные величины е, u, i в каждый момент времени при суммировании равны нулю. Иначе говоря: uА+uВ+uС=0.
Для примера демонстрируем вычисления сумм ЭДС при трех значениях углов:
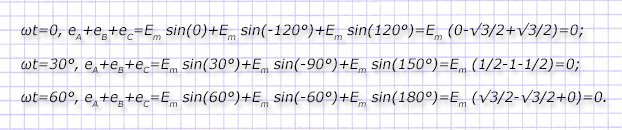
При равной нагрузке для каждой фазы, когда ZA=ZB=ZC=Zejφ, формируются одинаковые по длине, но сдвинутые по углу от напряжений (ЭДС) вектора фазных токов. Они разнесены между собой на 120° и тоже создают 3-х фазную симметричную систему, в которой действуют законы:
iA+iB+iC=0; IA+IB+IC=0.
Из трех не связанных систем формируется единая связанная путем подключения (объединения) обратных (возвратных) проводов в единую магистраль. При этом способе в обобщенном проводе общий ток от трех фаз сложится и станет равным нулю. Процесс описывает 1-й закон Кирхгофа:
iN=iA+iB+iC=0.
Практический вывод очевиден: отсутствие необходимости обратного провода, что ведет к значительной экономии материальных средств для транспортировки электроэнергии от 3-х фазного генератора к 3-х фазному электроприемнику.
Преимущества 3-х фазных систем:
1. Транспортировка электрических мощностей 3-х фазной схемой к потребителям от источников экономически эффективнее, чем для другого количества фаз. При снижении количества магистралей с 6 до 3 не только экономятся средства на провода, но и снижаются энергетические потери в них;
2. Для создания 3-х фазной системы не требуется создавать сложных технических конструкций. Круговое вращательное движение давно используется для работы различных генераторов и двигателей;
3. Технология изготовления 3-х фазных генераторов, трансформаторов и двигателей проста и отлажена, а все устройства отличаются надежностью, долговечностью, дешевизной и уменьшенными габаритами;
4. 3-х фазная схема позволяет одновременно применять электрические приемники с разными номиналами напряжений, отличающимися на величину √3, которая определяется наличием 2-х уровней напряжений (фазного и линейного). Uл=√3xUф.
Эти очевидные преимущества систем широко используются в энергетике для выработки электрической энергии и передачи/распределения ее к электроприемникам с 1989 года.
Основоположником и разработчиком их является инженер Михаил Осипович Доливо-Добровольский, работавший в немецкой фирме AEG (Allgemeine Elektricitäts-Gesellschaft).