Способы расчетов схем синусоидальных токов с помощью законов Кирхгофа

Мгновенные значения синусоидальных гармоник токов, ЭДС и напряжений удобно рассчитывать, используя знания законов Кирхгофа.

Первый закон определяет равенство нулю алгебраической суммы всех величин токов в точке узла для любого момента времени, а второй — всех величин ЭДС и напряжений на всех участках для замкнутого контура в любой момент времени. Они выражаются математически:

n - количество ветвей электрической цепи, m - количество ветвей, образующих контур цепи.

Синусоидальные гармоники токов, ЭДС и напряжений являются функциями времени, выражаются в декартовых координатах проекциями векторных величин на координатные оси. Вектора можно записывать комплексными числами. При сложении векторных величин производится сложение их проекций. Формулы для сложения:

Для проведения расчетов в цепях синусоидальных гармоник можно пользоваться одним из трех методов:

1. Применять способы векторных диаграмм;
2. Использовать для определения неизвестных величин приведенные ранее формулы Кирхгофа;
3. Выбирать для расчетов преобразования уравнений в комплексных чисел для символического метода.

1-й вариант расчета сходящихся в одном узле трех ветвей с двумя известными гармониками методом сложения:

   i₁=5sin(ωt+24O) A;
   i₂=3sin(ωt+116O) A.

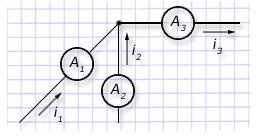Третий ток i₁ нам не известен, его значение следует определить и записать выражением.

Решаем задачу следующей последовательностью действий:

   i₃=i₁+i₂=5sin(ωt+24O)+3sin(ωt+116O)=I_3msin(ωt+Ψ₃).

Синусоидальные гармоники с одной частотой при суммировании дадут синусоиду такой же частоты, а значение ее амплитуды с начальной фазой рассчитываются по математическим законам:

   I_3m=√[I_1m²+I_2m²+2I_1mI_2mcos(Ψ₁-Ψ₂)]= √[52+32+2∙5∙3∙cos(24-116)]=5,74.
   tgΨ₃=(I_1msinΨ₁+I_2msinΨ₂)/(I_1mcosΨ₁+I_2mcosΨ₂)=(5sin24+3sin116)/(5cos24+3cos116)=1,454, Ψ3=55,5°.

Получаем: i₃=5,74∙sin(ω_t+55,5).

2-й способ определения посредством использования операций с векторами. По выражениям 1-го закона Кирхгофа имеем:

   Ī_3m=Ī_1m+Ī_2m.

В декартовых координатах выстраиваем вектора Ī_1m и Ī_2m, суммируем их и находим искомый Ī_3m:

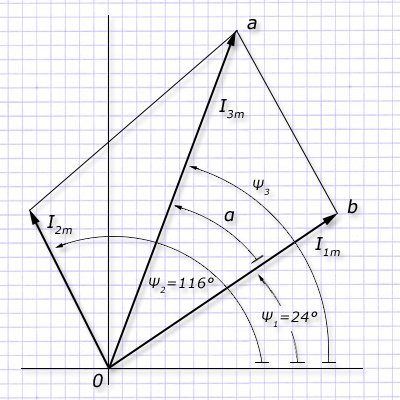
Если бы угол b треугольника оab был прямой, то протяженность ab выражала бы длину вектора I_2m. Тогда можно бы было найти его сторону по двум известным через теорему Пифагора:

   I_3m=√(I1_m²+I2_m²).

В нашем случае приходится использовать теорему косинусов. Она позволяет определить косинус вектора I_3m разностью косинусов векторов I_1m и I_2m с учетом знаков, а по значению косинуса вычислить угол 55,5° и длину вектора. В нашем случае она равна 5,74А.

3-й способ основан на решении той же символическим методом. Для этого надо записать формулами комплексные амплитудные значения всех известных величин:

   İ_1m=5e^j24°=5(cos24°+jsin24°)=4,568+j∙2,034 A;
   İ_2m=3e^j116°=3(cos116°+jsin116°)=-1,315+j∙2,696 A.

Применяем 1-й закон Кирхгофа для расчета третьего тока в символической форме:

   İ_3m=İ_1m+İ_2m=(4,568-1,315)+J(2,034+2,696)=3,253+j∙4,73=5,74 e^j55,5° А.

Модуль 5,74 равен амплитуде искомого тока, а его аргумент 55,5° – углу отсчета (величине) начальной фазы.

Чтобы определить действующие значения (в виде показаний амперметров) для каждой цепи надо перейти к выражению действующих значений, по которым работают приборы электромагнитных систем.

   I₁=I_1m/√2=5/√2=3,541;
   I₂=I_2m/√2=3/√2=2,125;
   I₃=I_3m/√2=5,74/√2=4,065.

Подведем итоги. Данные вычисления наглядно демонстрируют, что простое арифметическое сложение первых двух синусоидальных токов не позволяет точно определить значение третьего и создает большую погрешность. Для сложения гармоник синусоид действуют более сложные, описанные выше правила.

После проведения расчетов по 3-м способам можно сделать вывод о громоздкости 1-го, сложности вычисление и манипуляции с синусоидами. Поэтому им пользуются довольно редко.

2-й метод более удобен для простых задач, а 3-й позволяет рассчитывать линейные цепи любой степени сложности.