3-х фазные трансформаторы, электродвигатели и другие электроприемники подключаются к выводам генераторов по схеме звезды (γ) либо треугольника (Δ). При этом учитываются следующие особенности:
- линейные и фазные величины напряжений генератора отличаются в 1,732 раза. Uл=√3Uф;- конструкция электроприемника выполнена для работы с определенным напряжением, называемым номинальным. Его требуется подключать к соответствующим выходным цепям генератора.
Именно поэтому, необходимо выбирать оптимальное соотношение между номинальными величинами напряжений генератора и нагрузки при выборе схемы соединения фаз.
При равенстве номинального напряжения нагрузки, фазным значениям генератора выбирается схема звезды. При этом способе выхода с обмоток приемника подключаются к общей точке "N", которую именуют нейтральной либо нулевой.
Входы с обмоток (начала фаз) коммутируют к линейным клеммам 3-х фазного генератора A, B и C соединительными проводниками.
Варианты подключения по схеме звезда:
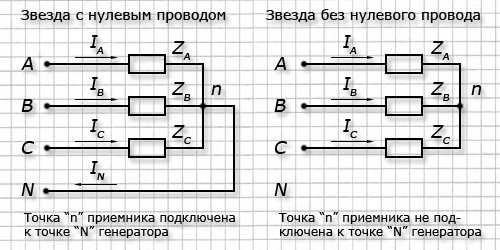
В соединительных проводах между генератором и приемником протекают токи. Их называют линейными токами.
В обмотках приемников тоже протекают токи, которые получили название фазных. Их направление от начала (входа в обмотку) к концу (выходу) считается положительным (+).
При последовательном подключении фаз нагрузки к линейным проводам генератора в образовавшейся цепи циркулируют одни и те же электротоки IА, IВ и IС. Они в схеме звезды равны для линии и обмоток приемника, другими словами: Iл= Iф.
У схемы звезды с нулевым проводом в нейтрали протекает нулевой (не значит, что его значение равно нулю) или нейтральный ток, обозначаемый IN.
Возникающую при прохождении тока разность потенциалов между началом и окончанием каждой обмотки в приемнике называют фазным напряжением, обозначают UАN, UBN и UCN.
Разности потенциалов между точками подключения начала фаз называют линейными напряжениями, обозначают UАВ, UBС и UCА. Их значения одинаковы для генератора и нагрузки.
У электроприемников схемы звезды с нулевым проводником для любой обмотки подключается соответствующее фазное напряжение от генератора. Оно обозначается для фазы:
А: UАN=UАN= UА; В: UВN=UВN=UВ; С: UСN=UСN=UС.
Любая фаза работает самостоятельно, не зависит от других. В ней токи (линейные или фазные) определяют формулой по закону Ома:
IА=UА/ZА; IВ=UВ/ZВ; IС=UС/ZС.
Первый закон Кирхгофа позволяет определить ток в нейтральном проводе как геометрическую сумму линейных либо фазных токов выражением: IN=IA+IB+IC.
При равных и симметричных нагрузках (ZA=ZB=ZC) величина тока в нейтральном проводе равна нулю. IN=0. Поэтому, симметричные 3-х фазные электроприемники (электродвигатели) подключают без нейтрального провода.
Для случая нарушения симметрии нагрузки характерно появление в нулевом проводнике тока, величина которого определяется отличиями от симметричных составляющих.
Такие отклонения снижают на стадии проекта и производства, чем и объясняются незначительные величины токов в нулевом проводе по сравнению с фазными/линейными значениями.
Описываемые 1-м законом Кирхгофа соотношения токов для любых нагрузок схем звезды без нулевого провода (IA+IB+IC=0) определяют взаимозависимость векторов.
Изменение одного любого вектора ведет к одновременному преобразованию остальных, чем проявляется зависимость режима. Ток нейтрали формирует разность потенциалов с величиной отличной от нуля.
На комплексной плоскости напряжение нулевой последовательности изображается вектором Un, смещающим центральную точку соединения векторов фазных напряжений для приемника (UАN, UВN, UСN), которые теряют равенство с фазными напряжениями генератора (UА, UВ, UС). Возникает перекос с фазными напряжениями у приемника.
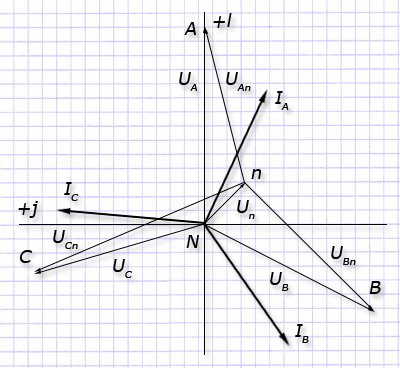
Способ расчета векторов тока и напряжения для схемы звезды без нулевого провода. Методом 2-х узлов вычисляются параметры смещения нейтральной точки для вектора напряжения нейтрали (UN):
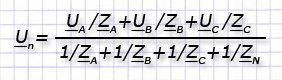
ZN – значение комплексного сопротивления нейтрального провода. Для схемы без нулевого провода ZN=∞.
Определение фазных напряжений основано на вычислении разности потенциалов между началами и окончаниями обмоток:
UАN=UА-UN; UВN=UВ-UN; UСN=UС-UN.
Расчеты фазных токов внутри приемника производятся на основе закона Ома:
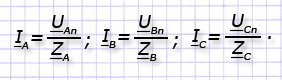
Величина тока в нейтральном проводнике вычисляется геометрической суммой входных линейных/фазных токов на основе 1-го закона Кирхгофа:
IN=IA+IB+IC.
Формулы для расчета полной мощности в фазах:
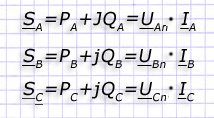
При разных нагрузках в фазах возникает перекос напряжений в схеме, который может привести к неисправностям. Поэтому, эксплуатировать такие нагрузки в схемах электроприемников без нулевого провода (часто это коммутируемые цепи освещения, обогрева и др.) запрещено.
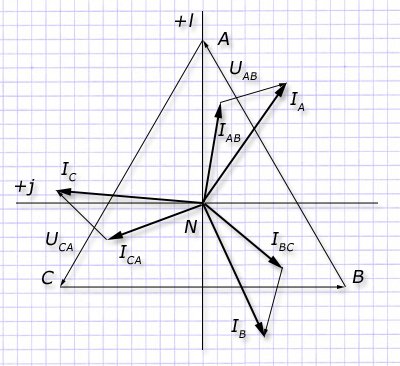
Способ расчета векторов тока и напряжения для схемы треугольника. При равенстве значений номинальных напряжений электроприемника величинам линейных напряжений генератора используется схема треугольника.
Для ее создания в приемнике выход одной обмотки подключается ко входу другой с выводом точки коммутации (являющейся вершиной треугольника) на клемму для соединения проводами с линейным выводом 3-х фазного генератора. Так формируются подключения к фазам А, В, С.
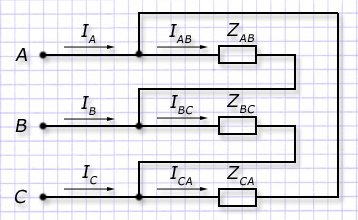
В обмотках такого приемника проходят фазные токи IАB, IBC, ICА. А токи, подводимые к приемнику от генератора по проводам, называют линейными. Их обозначают IА, IB, IC.
Для рассматриваемой цепи выполняется равенство подводимых напряжений с линии фазным напряжениям приемника UАB, UBC, UCА. Каждая отдельная фаза работает самостоятельно без зависимости от остальных.
Расчет фазных токов проводится по закону Ома:
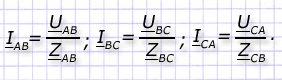
Вектора линейных токов описываются 1-м законом Кирхгофа в точках вершин треугольника и вычисляются как геометрическая разность векторов в фазах:
IА=IАB-IСА; IВ=IBС-IАВ; IC=IСА-IВС.
Для симметричного режима нагрузок выполняется симметричность фазных и линейных токов, которые определяются соотношением Iл=√3Iф. При несимметричном режиме нагрузок соотношения векторов линейных и фазных описываются 1-м законом Кирхгофа.
Примерное соотношение векторов для произвольной 3-х фазной цепи, работающей по схеме треугольник на комплексной плоскости, представлено на векторной диаграмме.