Рассмотрим вариант параллельного подключения индуктивных потребителей к источнику с синусоидальным напряжением. Обмотки у катушек №1 и №2 характеризуются электрическими значениями активных сопротивлений (R1, R2) и индуктивных — (L1, L2) соответственно. Величину взаимоиндукции между ними обозначим индексом M.
В статье изучим два метода соединения катушек между собой с учетом направления провода навивки или, говоря по-другому, варианта коммутации входных клемм. У обмоток катушек выводы полярных концов обозначим знаком "*".
Ниже приведены способы согласованного (1) и встречного (2) подключения обмоток:
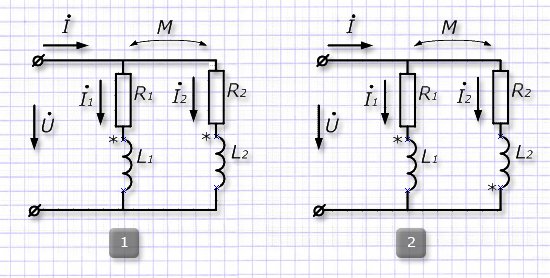
Для обеих этих цепей напишем уравнения, описываемые 2-ым законом Кирхгофа.
Ù=Z1·İ1±··İ2; Ù=Z2·İ2±ZM·İ1.
После их решения получим следующие соотношения для векторов токов.
Ì1=Ù·(Z2±ZM)/(Z1·Z2-Z2M), Ì2=Ù·(Z1±Z2M)/(Z1·Z2-Z2M), Ì=Ì1+Ì2=Ù·(Z1+Z2±2ZM)/ (Z1·Z2-Z2M).
Для данных выражений приняты соотношения:
Z1=R1+jωL1, Z2=R2+jωL2, ZM=R1+jωLM.
Выведем значение комплексного сопротивления на входе схемы как отношение приложенного напряжения к величине тока протекающего по цепи.
Z=Ùİ=(Z1·Z2-Z2M)/(Z1+Z2±2ZM).
Данное соотношение позволяет демонстрировать исключение влияния взаимоиндукции на каждую обмотку катушек (когда справедливо значение ZM=0). Подставив его в представленную формулу, получим выражение для сопротивлений с 2-мя типичными параллельными цепочками вида:
Z=Z1·Z2/(Z1+Z2).
Внимание! У вышеприведенных соотношений применены слагаемые с удвоенными знаками, имеющие вид символа ±. У него верхний знак обозначает последовательность вычислений для согласованного подключения нагрузок, а знак нижний — встречного.
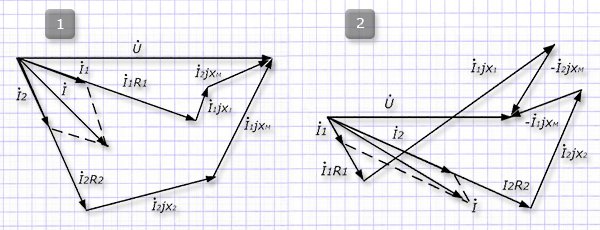
У рассматриваемых нами цепочек картинка для векторных диаграмм представлена ниже (1 - согласованная схема, 2 - встречная схема):