Способы расчета схем параллельного соединения активного сопротивления с индуктивностью и емкостью

Выберем для рассмотрения схему параллельного подключения к выходным контактам источника переменного напряжения к активному и реактивному сопротивлениям. В качестве реактивной нагрузки используем параллельное подключение индуктивности L с конденсатором С.

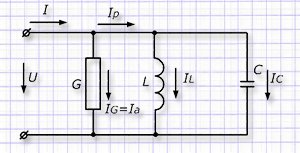
Используем символ "G" для обозначения проводимости у активного сопротивления, а значения "В_L" и "В_C" — для проводимостей в катушке индуктивности и конденсаторе соответственно.

На вход схемы подается синусоидальное переменное напряжение U. Нам требуется выяснить картину распределения токов по элементам всей схемы. Решим поставленную задачу двумя простыми методами.

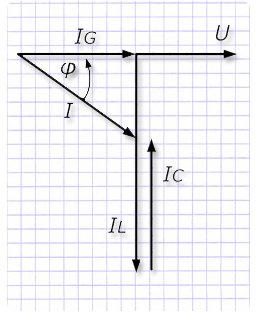Способ векторных диаграмм. На представленной схеме видно, что на все элементы подается одно напряжение U. Зная величины проводимостей, определим значения токов в каждом элементе:

   I_G=GU;   I_L=B_LU   I_C=D_CU.

Нам требуется рассчитать токи для всей схемы. С этой целью строим векторную диаграмму, причем за ее основу используем общий для всех элементов вектор напряжения U.

Ток у активного сопротивления совпадает своим направлением с вектором напряжения. Из его конца направляем вектор тока катушки индуктивности с опережением по вращению на 90°, а из его окончания начинаем построение вектора в конденсаторе с отставанием на 90° от вектора приложенного напряжения.

Результирующий вектор I определится геометрической суммой составляющих векторов:

   I=√[I_G²+(I_L-I_C)²]=√[(G∙U)²+(B_L∙U-B_C∙U)²].

Представим I=у∙U, где символом "у" обозначена общая проводимость всей цепи. Ее удобно представить выражением:

   y=√(G²+(B_L-B_C)²)=√(G²+B²).

Величина В выражает полную составляющую реактивной проводимости элементов цепи.

   В=В_L-В_C.

Из векторной диаграммы хорошо видно, что в нашем случае токи образовали прямоугольный треугольник. У него горизонтальным катетом представлена активная составляющая, равная току, проходящему по активному сопротивлению I_А=I_G=G∙U. А реактивная составляющая Īр образована суммой токов в индуктивности и емкости.

   Ī_P=Ī_L+Ī_C.

Она выражает проекцию результирующего вектора I на вертикальную ось (перпендикулярное направление к вектору напряжения).

При идеальном случае значение I_P можно вычислить как разность длины векторов тока на индуктивности и конденсаторе.

   I_P=I_L-I_С=В_L∙U-В_С∙U=(В_L-В_С)∙U=В∙U.

Для данного случая можно представить треугольники тока (рис. 1) проводимостей (рис. 2) и токов.

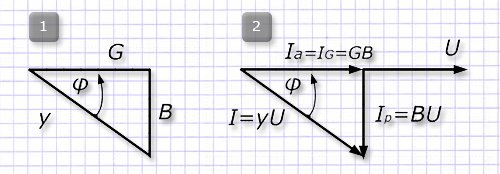
Причем, треугольник проводимостей получается простым делением сторон треугольника токов на общее для всех элементов значение напряжения U. Соотношения сторон связаны тригонометрическими выражениями:

   cosφ=G/y;   sinφ=B/y;   tgφ=B/G;   y=√(G²+B²).

Символический метод. Воспользуемся ранее полученными формулами:

   Ì_G=GÙ;   Ì_L=-ÙjB_L;   Ì_C=ÙjB_C.

Подставим их в выражение 1-го закона Кирхгофа для нашей схемы:

   Ì=Ì_G+Ì_L+Ì_C=Ù(G-jB_L+jB_C).

Используем выражение Ì=ÙY, в котором величиной Y обозначим комплексную проводимость всей цепи. Она определяет

   Y=G-j(B_L-B_C)=G-jB=ye^-jφ.