Расчеты режимов трехфазных симметричных нагрузок при несимметричных напряжениях

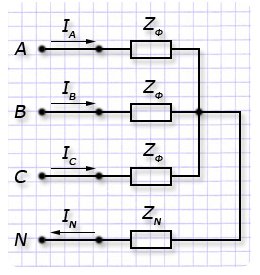
Рассмотрим момент подключения к несимметричным системам напряжений U_A, U_B, U_C 3-х фазных электродвигателей, как симметричных электроприемников с определенным сопротивлением Z_N в нейтральном проводе по схеме:

Преобразуем напряжения несимметричной системы в виде симметричных составляющих прямой, нулевой и обратной последовательностей выражениями для векторов напряжений фазы A:

   U_А1=(UU_А+аU_Bа²U_C)/3;
   U_А2=(U_А+а²U_BаU_C)/3;
   U_А1=(U_А+U_B+U_C)/3.

Пользуясь методом наложения, рассчитываем токи каждой составляющей напряжений. Учитывая симметрию системы, определяем токи режимов только в рассматриваемой фазе. Потом делаем перерасчет для трехфазной системы.

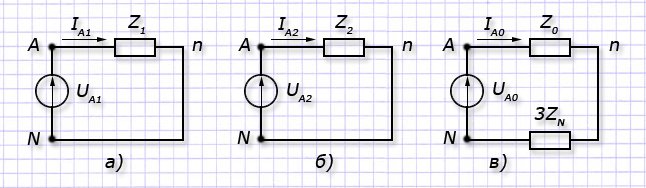
Для режимов чередования прямой и обратной последовательностей характерно отсутствие токов через нейтральный провод, что исключает падение напряжения в нем.

Поэтому, величина U_nN=0 и можно учитывать, что полное сопротивление у нейтрального провода Z_N=0 не влияет на значения фазных токов для этих режимов. Его не включают в схему и не учитывают в формулах.

У режима нулевой последовательности характерно то, что ток каждой фазы аналогичен токам других фаз, проходит через нейтральный провод. I_N=I_A0+I_В0+I_С0=3I_A0. Поэтому, напряжение, создаваемое от тока нулевого провода, описывается 2-м законом Кирхгофа:

   U_А0=I_A0Z₀+I_NZ_N=I_A0(Z₀+3Z_N).

Таким образом, для нулевой последовательности формируется схема замещения с последовательным подключением к сопротивлению каждой фазы Z₀ утроенного сопротивления нейтрали 3Z_N.

В режиме каждой последовательности у приемника с вращающимся полем комплексные сопротивления Z1, Z2 и Z0 в одних и тех же фазах разные, отличаются значительно, позволяют рассчитывать по закону Ома токи для каждого режима.

   I_A1=U_A1/Z1;     I_A2=U_A2/Z2;     I_A0=U_A0/(Z₀+3Z_N).

Значение действительных токов в реальной системе определяется по способу наложения с учетом векторных сумм каждого режима;

   I_А=I_А1+I_А2+I_А0;
   I_В=I_В1+I_В2+I_В0=а²I_А1+аI_А2+I_А0;
   I_С=I_С1+I_С2+I_С0=аI_А1+а²I_А2+I_А0.

Существующие статичные 3-х фазные электроприемники в виде приборов освещения, обогрева и прочего подобного оборудования обладают комплексным сопротивлением в фазах, которое не зависит от вида последовательности чередования.

Для них выполняется соотношение: Z1=Z2=Z3, а значения токов в них легче определять обычными способами расчетов.

У 3-х фазных электроприемников (двигателей и генераторов) с вращением магнитного поля характерно отличие параметров комплексных сопротивлений фаз для каждого режима. Причем Z2<Z0<Z1. Их расчеты проводятся только по методике симметричных составляющих.