Обыкновенный трансформатор, широко используемый в электротехнике, имеет довольно простое устройство. В его конструкцию включен магнитопровод из стальных сплавов с определенными магнитными свойствами и две катушки, которые обычно выполняют в виде обмоток из изолированного провода.
Их помещают в отдельный корпус либо навивают прямо вокруг изоляционного материала сердечника. Концы проводов выводят на клеммы, которые маркируют для обозначения полярности.
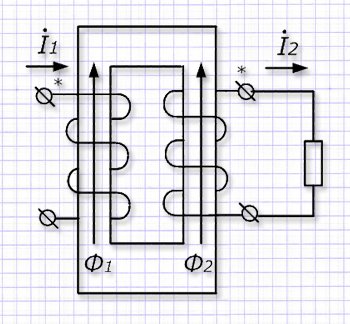
Из двух обмоток одна подключается к напряжению первичной питающей сети. По ней протекает ток İ1 с величиной зависящей от полного сопротивления первичной обмотки, внутри которой и, естественно, сердечника магнитопровода формируется магнитный поток Ф1.
Он проходит по пластинам сердечника и пересекает своими силовыми линиями витки вторичной катушки, в которой создается ток I2.
В результате создается поток Ф2, имеющий встречное направление потоку первичной обмотки. Природа описанного алгоритма хорошо объясняется правилами Ленца и правой руки.
Все виды ферромагнитных сердечников обладают магнитным сопротивлением определенной величины, которое обуславливает появлений нелинейных искажений у направления и значения вторичного тока, сказывается на точности трансформации.
Поэтому, от них отказываются для работы с высокими частотами и на устройствах, требующих точных метрологических характеристик.
Схема замещения подобного устройства представлена на рисунке с активными и индуктивными сопротивлениями в обеих обмотках и нагрузке.
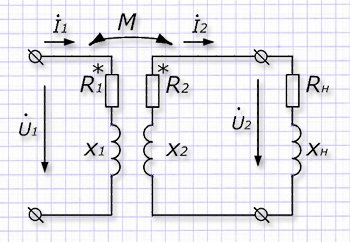
Упростим для рассмотрения схему вводом в нее дополнительных терминов:
R22=R2+RН; X22=X2+XН; ZН=RН+jXН; Z22=R22+jX22.
Они используются для обозначения суммарных активных и реактивных сопротивлений у выходной обмотки, комплексных сопротивлений выходной цепи.
Схема показывает встречное подключение между обмотками трансформатора. Применяем к ней 2-й закон Кирхгофа и составляем выражения:
Ù1=İ1·(R1+jx1)-İ2jxM; Ù0=İ2·(R2+jx2+RН+jxН)-İ1jxM.
В результате преобразования получим:
Ù1=İ1Z1-İ2ZM; Ù0=İ2Z22-İ1ZM.
Учтем, что I1jXM=E2M. В то же время, E2M=I2Z2+I2ZН.
Физический смысл данного выражения трактуется следующим образом: ЭДС E2M, наведенная магнитным полем первичной катушки во вторичной обмотке, расходуется на падение напряжений на всех элементах выходного контура.
Знаем, что I2ZН=U2. Получаем: U2=E2M-I2Z2.
Это выражение позволяет сделать вывод: выходное напряжение, создаваемое на клеммах вторичной обмотки, уменьшено от величины, выработанной в ней ЭДС, на значение падения напряжения от ее сопротивления.
Векторную диаграмму трансформатора представляет следующий рисунок:
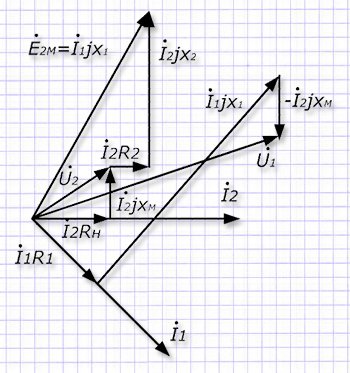
Его построение начинается от вектора I2 (тока во вторичной цепи), который определяет направления векторов напряжений на элементах выходной схемы, которые при суммировании создают величину вектора ЭДС E2M. Его поворот (отставание от тока I2 на часть периода) обусловливает составляющая j.
Направление для вектора тока I1 выбираем в сторону опережения от E2M на 90°. По нему строим вектора падения напряжения I1R1 и I1jX1, создающие при суммировании с I2jXM вектор U1.
Анализируя работу трансформатора удобно использовать приемы замещения основной схемы соединения эквивалентным аналогом. Рассмотрим один из подобных вариантов способом 2-х контурной или T-образной схемы. Для этого соединим закороткой оба его выходных (нижних) вывода. Это не нарушает режим работы трансформатора.
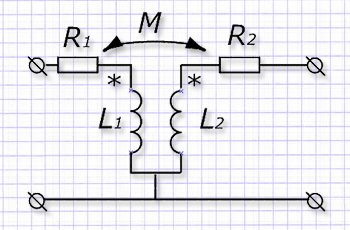
Далее проводим простую развязку у индуктивных связей и переходим на T-образную эквивалентную схему:
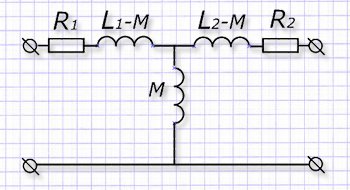
Теперь можно выделить из 2-го уравнения системы выражение тока I2 для подстановки его в 1-ое уравнение. В итоге выходит:
Ùİ2=İ1·(ZM/Z2)→Ù1=İ1Z1-İ1·(Z2M/Z2)=İ1·(Z1+ZВН).
Полученное последнее выражение описывает нарисованную нами эквивалентную схему, в которой последовательно подключенное сопротивление ZВН к Z1 называют термином вносимого сопротивления. Понимаем, что оно как бы перемещается в трансформаторе из выходной схемы в первичную цепь.
Его доступно выразить следующим образом:
ZВН=-(Z2M/Z2)=-((jxM)2/(R2+jx2))·((R2-jx2)/(R2-jx2))=(R2x2M-jx2x2M)/(R22+x22).
Наглядно видны активные и реактивные составляющие:
RВН=R2x2M/(R22+x22), xВН=x2x2M/(R22+x22).
На основании приведенного соотношения заметно, что в первичном контуре у активного сопротивления появилась составляющая от выходной схемы.
Это свидетельствует о расходе подводимой к трансформатору энергии не только на преодоление сопротивления во входной схеме, но и на сопротивления R2 и RН вторичной цепи, на которые она поступает посредством электромагнитных преобразований в обмотках и сердечнике.
Обратим внимание на отрицательный знак у вносимой реактивной составляющей сопротивления. Благодаря его наличию, уменьшается значение общего реактивного сопротивления всей схемы (состоящее из суммы Х1 и ХВН) и становиться меньше, чем индуктивное сопротивление в первичной обмотки.
Объяснение сказанного довольно простое: обмотки соединены встречно и магнитный поток Ф2противоположен потоку Ф1. Поэтому, снижая его значение, одновременно понижает общее индуктивное сопротивление.