Способы вычислений мощности трехфазной цепи

Вычисление величины полной мощности. Расчет полной мощности электрической цепи требует знания ее активной и реактивной составляющих, соотношение которых в любой схеме описывается треугольником мощностей.

Для вычисления активной (Р) и реактивной (Q) составляющих 3-х фазной цепи проводится суммирование их величин в каждой фазе по формулам:

   Р=Р_A+Р_B+Р_C=U_AI_Acosφ_A+U_ВI_Вcosφ_В+U_СI_AСcosφ_С;
   Q=Q_A+Q_B+Q_C=U_AI_Asinφ_A+U_ВI_Вsinφ_В+U_СI_AСsinφ_С.

I_A, I_В, I_С, U_A, U_В, U_С – вектора токов и напряжений в фазах,
Φ – угол сдвига фаз векторов тока относительно напряжения.

Для симметричного режима работы схемы во всех фазах выполняется равенство мощностей. Поэтому общую величину мощности можно получить простым умножением фазной составляющей на количество фаз в системе:

   Р=3Р_Ф=3U_Ф∙I_Ф∙cosφ;
   Q=3Q=3U_Ф∙I_Ф∙sinφ;
   S=3S_Ф=(Р2+Q2)=3U_ФI_Ф.

Делаем замену фазных составляющих линейными по их соотношениям для схемы звезды: I_Л=I_Ф, U_Ф=U_Л/√3.

В результате получаем:

   Р=3U_Ф∙I_Ф∙cosφ=(3U_Л∙I_Л/√3)∙cosφ=√3∙U_Л∙I_Л∙cosφ.

Заменяем фазные составляющие линейными для схемы треугольника по их соотношениям: I_Ф=I_Л/√3, U_Ф=U_Л.

Итог вычисления:

   Р=3U_Ф∙I_Ф∙cosφ=(3U_Л∙I_Л/√3)∙cosφ=√3∙U_Л∙I_Л∙cosφ.

Таким образом, получилось, что зависимость от вариантов соединения элементов цепи схемой γ либо Δ в 3-х фазной симметричной системе значения мощностей отсутствует. Они вычисляются по одним и тем же формулам:

   Р=√3∙U∙I∙cosφ [Вт];
   Q=√3∙U∙I∙sinφ [вар];
   S=√(Р²+Q²) [ВА].

Для данных выражений сложилось правило: подставлять линейные значения векторов U и I без указания их линейных индексов.

Способы измерений мощности В энергетике существует постоянная необходимость измерения электрических величин. Активная составляющая полной мощности замеряется ваттметром, а реактивная – варметром. Ваттметр работает по алгоритму, описанному формулой:

   W=U_W∙I_W∙cos(U_W^I_W)=Re│U_W∙I_W*│.

U_W, I_W – те вектора, которые подвели к клеммам прибору для замера активной составляющей.

Практика электрических измерений предлагает несколько вариантов подключения к электросети ваттметров. Они выбираются в зависимости от схемы выполненный коммутации нагрузок и ее характеристик.

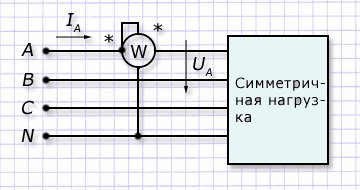
В симметричной 3-х фазной системе достаточно включить один ваттметр в любую фазу для постоянного замера активной мощности с последующим утроением полученного результата по алгоритму Р=3W=3U_Ф∙I_Ф∙cosφ.

Однако, этот простой способ только ориентировочно оценивает замеряемые величины, имеет большие погрешности. Поэтому, он малоприемлем для выполнения замеров, требующих высокой точности и в решении коммерческих задач.

Более точные замеры активной составляющей для звезды с нейтральным проводом обеспечивает использование в измерении трех ваттметров.

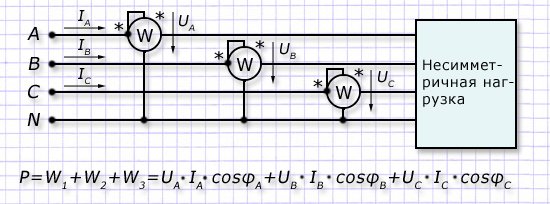
Выполняемые отдельно в каждой фазе измерения обладают большей точностью. Сложение показателей всех трех ваттметров предоставляет информацию об активной мощности с минимальными погрешностями.

При несимметричной нагрузке в 3-х фазной сети без нейтрального провода применяется способ замера двумя ваттметрами.

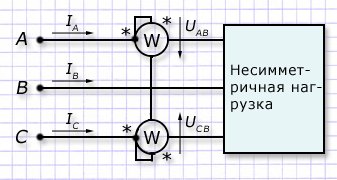
Особенность замера состоит в том, что линейные/фазные токи в такой электрической цепи взаимосвязаны 1-м законом Кирхгофа, когда их сумма I_А+I_В+I_С=0. Если математически сложить показания обоих ваттметров и описать их математическими методами, то получим выражения:

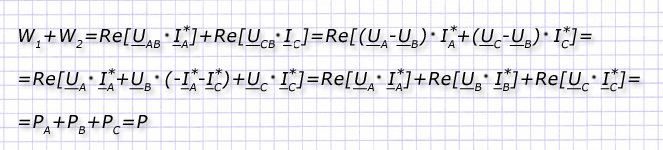
В итоге, подтвердилось предположение, что два ваттметра замеряют активную мощность данной схемы при суммировании их показаний. На показания любого из них влияют характеристики и величины нагрузок.

Вид векторов напряжений и токов на комплексной плоскости для симметричной нагрузки демонстрирует диаграмма:

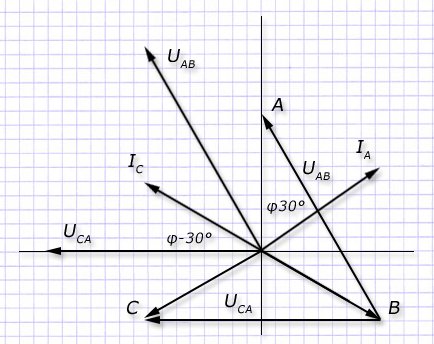
Из которой понятно, что для обеспечения показаний ваттметров используются выражения:

   W₁=U_Л∙I_Л∙cos(φ+30°);
   W₂=U_Л∙I_Л∙cos(φ-30°).

По результатам анализа данных формул достаточно несложно сделать следующие выводы:

1. При φ=0 создается равенство показаний обоих ваттметров, что весьма характерно для чистой активной нагрузки;

2. Когда 0≤φ≤90° (четверть активно-индуктивной нагрузки квадранта) показания 2-го ваттметра больше, чем первого (W2>W1). В этом же квадранте все показания у 1-го ваттметра приобретают отрицательную величину при значениях φ>60°;

3. В случае 0≥φ≥90° (четверть активно-емкостной нагрузки квадранта) показания 1-го ваттметра больше, чем второго (W1>W2). В этом же квадранте показания 2-го ваттметра приобретают отрицательную величину при значениях φ<-60°.